Collective phenomena

This research focuses on nonlinear waves obtained in photonic system and the emergence of  collective phenomena, phase transitions and photonic complexity. In this context, complexity may arise due to widely differing time scales or interaction of small or large number of elements or degrees of freedom which can be induced by spatial extension or delay for instance.

Neuromorphic photonics

One key research area is neuromorphic photonics, which I wish to take from hardware models of neurons to photonic AI. One interesting architecture is that of coupling a "neuron-like" laser to itself after a delay, in a configuration which is sometimes called "autaptic". Starting from our earlier work demonstrating the storage of data in such a configuration (_ie_ a _memory_) we have recently studied the effect of interactions between spikes in such a system. One key result is that interactions can lead to a transition from ordered to disordered behavior, as illustrated on "transition.png": Many spikes are initially synchronized to an external clock but when the number of spikes changes too much, the much weaker interactions (due to larger average distance) lead to collective motion of spikes which do not remain locked to the external clock anymore. This transition is thus mediated _by the interactions among light spikes_, which makes it rather fascinating.

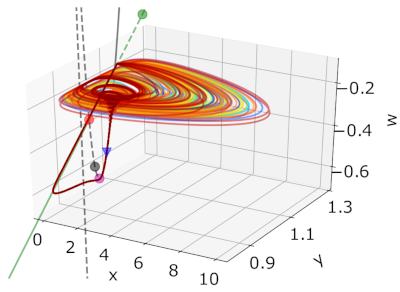
Along the same line of research, we have recently addessed the collective behavior of a large ensemble of coupled lasers submitted to opto-electronic feedback. There are many ways lasers or more generally photonic systems can be configured so that they mimick the behavior of neurons. However, isolated neurons do not accomplish much in the biological realm where even the simplest animals count with thousands of neurons. Similarly, the computer neural networks which we operate daily when interacting with smart devices easily count with tens of thousands of neurons. Thus, one key towards photonic AI is to operate _large networks_ of neuron-like elements. In a mean-field coupled network of 450 lasers coupled via nonlinear electro-optical feedback, we have shown (thanks to the slow-fast nature of the system) that most of the dynamics can be understood from the analysis of the network's critical manifold. This critical manifold is actually very close to that of a single node and we have recently shown that noise has a surprising streamlining effects on the dynamics. This phenomenon, which we have called _Canard Resonance_ leads the network to behaving in a most ordered way in presence of non-zero noise. The figure meanfield.png shows a numerical trajectory of the network: the critical manifold of a single device (the union of the dashed line and parabola) is heavily attractive for all of the network elements. In presence of noise, the whole network smoothly cruises around unstable branches of its critical manifold.

Laser mode-locking

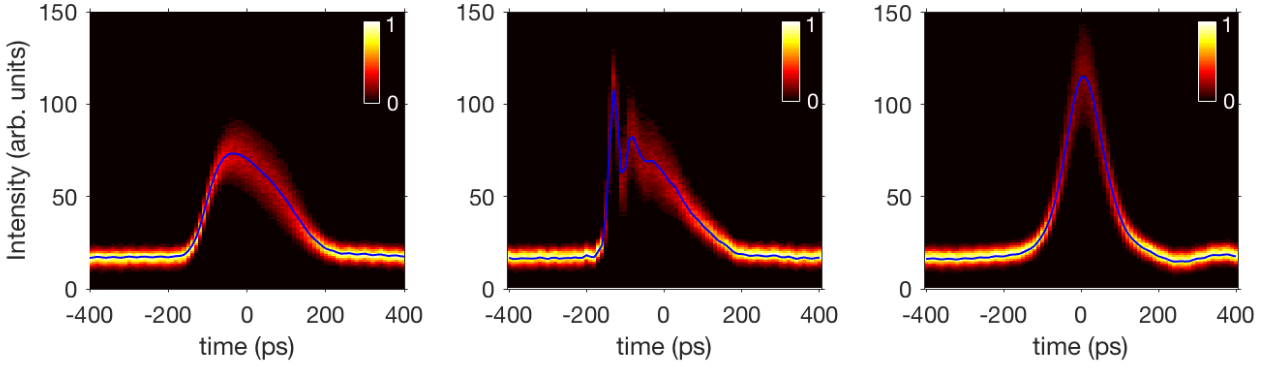
The line of research above has a very strong "dynamical systems" component, for which optical systems have long been fantastic test benches. In addition to that, lasers also display remarkable physical behaviors related to wave interactions, among which the famous regimes of "laser mode locking" and "laser threshold". Mode locking is perhaps the most useful of all laser regimes and certainely one of the most widely studied, including for instance in the context of localized states of light. To a very large extent, an excellent description of the laser mode-locking phenomenon has been provided by H.Haus with its seminal master equation for mode locking. At the opposite edge of the spectrum, fully developed Maxwell-Bloch equations can of course be used to model mode-locked lasers, at the expense of a very large computational and physical complexity. We have contributed to the analysis of an intermediate level of description which includes coherent light matter interaction (of course totally absent from Haus' master equation) and which may constitute an excellent trade-off between modelling complexity and physical richness: the _coherent master equation for mode locking_. While Haus master equation only leads to symmetrical pulse solutions, the _coherent master equation_ correctly reproduces the shape the pulses which are experimentally reported (master.png)

Thermalization in semiconductor microresonators

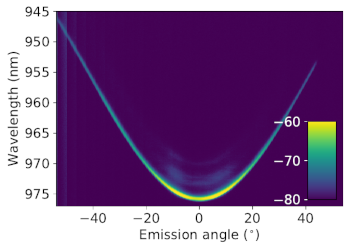
Even deeper at the roots of laser physics lies of course the celebrated _laser threshold_. Putting it simple, below that point, only spontaneous emission is observed and above that point a coherent field is emitted. This coherent state is constituted of a large number bosons in a single quantum state so of course, such a state of light bears some similarity to a Bose Einstein condensate of atoms. This parallel has long been known and it is commonly admitted that the laser phase transition is very similar to the Bose Einstein condensation phase transition, with the quite important difference that it takes place _outside of thermal equilibrium_. So the key question here is not about the laser state itself but instead it is about the process by which a coherent state can be obtained. In laser physics, the well established paradigm is that this state is reached when the gain compensates for the losses. In atomic BEC, it happens through a thermalization process at equilibrium and is reached when the phase space density is high enough so that there is significant overlap of the wave functions. We are interested in revisiting this physics in semiconductor microresonators _designed as lasers_. Figure mass.png shows the dispersion relation of light in a planar semiconductor resonator. In this device (a Vertical Cavity Surface Emitting Laser), we have shown that light can efficiently thermalize via interactions with electrons and holes. When phase space density is high enough, this leads to an accumulation of light in the lowest energy state, in strong analogy with atomic Bose Einstein condensation.

 

All the above research takes place in semiconductor photonic devices. However, it could not take place without interaction with researchers from other fields, namely applied mathematics, theoretical neuroscience or cold atoms. More generally, I strongly believe that fantastic sources of knowledge and inspiration can be found in neighbouring areas of research. Along this line of thought, we have organized in 2019 the first edition of the WAVESCOTEDAZUR conference (http://wavescotedazur.org waves_cote_d_azur.png), a transdisciplinary conference on nonlinearity and disorder in wave phenomena, from microscopic to physiologic and astronomical scales. In the same vein, we currently run the WAVECOMPLEXITY initiative, which aims at fostering cross-disciplinary progress on complex wave phenomena http://wavecomplexity.org.